컴퓨터에서의 데이터 표현
진법과 진법 변환
정수 표현
실수 표현
디지털 코드
에러 검출 코드
진법과 진법 변환
디지털 정보의 단위
1nibble = 4bit
1byot = 8bit
1byte = 1문자(character)
영어는 1byte로 1문자 표현, 한글은 2byte가 필요
1워드 : 특정 CPU에서 취급하는 명령어나 데이터의 길이에 해당하는 비트 수
워드 길이는 8, 16, 32, 64비트 등 8의 배수가 가능하다
진법(number system)
2 진법 : 0과 1 두가지 기호로 표현하는 수의 체계
8 진법 : 0,1,2,3,4,5,6,7의 8가지 표현하는 수의 체계
10진법 : 0,1,…,8,9의 10가지 기호로 표현하는 수의 체계
16진법 : 0,1,2,…,9,A,B,C,D,E,F 까지의 16가지 기호로 표현하는 수의 체계

진법의 변환
10진수 -> 2진수 (R 진수)

2진수 (R 진수) -> 10 진수

8/16 진수 <-> 2 진수

분수(실수)의 변환

보수 (Complement)
최대값 (해당 bit 에서 가장 큰 표현형)을 형성하는ㄴ데 서로 보완 관계에 있는 두 수 사이의 관계를 one's COMPLEMENT라고 한다
MODULUS (최대 표현 자리 수)를 형성하는데 서로 보완관계에 있는 두 수사이의 관계르 two's COMPLEMENT라 한다
ex) 10진수에서의 보수
- 1진 보수 (ONE'S COMPLEMENT) : A+B=9, A+B=99
- 2진 보수 (TWO'S COMPLEMENT) : A+B=10, A+B=100
ex) 2진수에서의 보수
- 1진 보수 (ONE'S COMPLEMENT) : A+B=1, A+B=11, A+B=111
- 2진 보수 (TWO'S COMPLEMENT) : A+B=10, A+B=100, A+B=1000
2진수의 1의 보수는 자신의 수를 반대 (1<->0)로 바꾸면 되고, 2의 보수는 1의 보수에 +1 또는 주어진 수의 우단으로부터 최초의 유효 BIT까지는 그대로 두고 나머지를 모두 반대 (1<->0)로 바꾸면 된다
정수 표현
정수형 (고정 소수점, FIXED POINT NUMBER) 표현
부호화 절대치 (SIGNED MAGNITUDE)
정수의 부호와 절대치를 따로 보관한다
(* 음수 표현은 절대치가 같은 양수와 부호만 다르다)
표현 범위 (n bit 사용)
+0 과 -0이 공존
보수(Complement)를 취하는 방법
R의 보수 R-1의 보수가 존재한다
양수의 표현은 절대값 표현 방식과 동일
표현 범위 (n bit 사용)
10진수형 정수 표현
* Unpacked decimal
zoned decimal 일하며 EBCDIC의 숫자 표현과 동일
1 byte ---> 10진수 한자만 표현
연산에는 이용 될수 없으나 입출력 가능
* packed decimal
1byte에 2자의 10진수를 표현 (BCD code 이용)
마지막 4개의 비트로는 부호를 표현
연산에 이용, 입출력 불가능
실수 표현 (부동 수수점, Floating-point)
과학적 표기의 지수(exponent)를 사용하여 소수점의 위치를 이동시킬 수 있는 표현 방법
표현의 범위가 확대
바트 수에 따른 분류가 가능하다4
- 단일 정밀도 부동 소수점 형식
- 부호 비트 : 0 / +
- 지수 (E) = 0000101 = 5
- 기수 (M) = 1001 0000 0000 0000 0000 -> + 01001 x 2ⁿ
디지털 코드
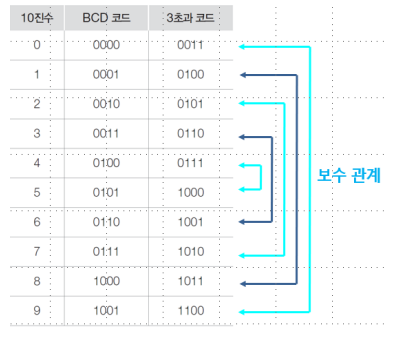
BCD 코드 (Binary Coded Decimal Code : 2진화 10진 코드, 8421 코드)

3초과 코드 (excesss-3코드)
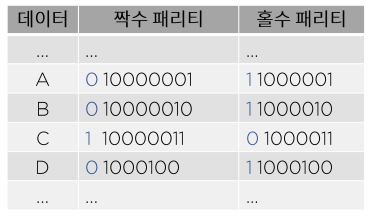
패리티 비트
해밍 비트 : 8비트 데이터의 에러 정정 코드
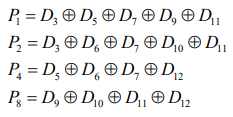
출처 : 제로베이스
'공부 Note > 컴퓨터 구조' 카테고리의 다른 글
| Chapter 02 데이터의 종류 (3) (0) | 2022.01.24 |
|---|---|
| Chapter 02 데이터의 종류 (2) (1) | 2022.01.24 |
| Chapter 01 컴퓨터 시스템의 이해 (4) (0) | 2022.01.19 |
| Chapter 01 컴퓨터 시스템의 이해 (3) (0) | 2022.01.19 |
| Chapter 01 컴퓨터 시스템의 이해 (2) (1) | 2022.01.19 |

