선형 자료 구조 ⭐
| 구분 | 설명 |
| 순차리스트 | 배열처럼 자료를 나열하여 메모리에 연속적으로 저장하는 형태 |
| 연결리스트 | 각 노드가 데이터와 포인터를 가지고 한 줄로 연결되어 있는 방식으로 데이터를 저장하는 구조 |
| 스텍 | 모든 원소들의 삽입과 삭제가 리스트의 한쪽 끝에서만 수행되는 제한조건을 가지는 구조 LIFO (Last In, First Out) |
| 큐 | 먼저 입력된 자료를 가장 먼저 처리하는 구조 한쪽 끝에서만 자료를 넣고 다른 한쪽에서만 자료를 빼낼 수 있는 구조 FIFO (First In, First Out) |
| 데크 | 큐 두 개 중 하나를 좌우로 뒤집어서 붙인 구조 큐의 양쪽 끝에서 삽입 연산과 삭제 연산을 수행할 수 있도록 만들어짐 큐와 스텍의 장점을 결합 |
트리 ⭐

| 구분 | 설명 |
| 노드 (node) | 트리의 원소 (A, B, C, D, E, F, G, H, I, J) |
| 간선 (edge) | 노드를 연결하는 선 |
| 루트 노드 | 트리의 시작 노드 (A) |
| 형제 노드 | 같은 부모 노드의 자식 노드들 (B, C) |
| 조상 노드 | 간선을 따라 루트 노드까지 이르는 경로에 있는 모든 노드들 (J의 조상 노드 : F, C, A) |
| 서브 트리 | 부모 노드와 연결된 간선을 끊었을 때 생성되는 트리 |
| 자손 노드 | 서브 트리에 있는 하위 레벨의 노드들 (C의 자손 노드 : F, G, J) |
| 차수 (degree) | 노드의 차수 : 노드에 연결된 자식 노드의 수 트리의 차수 : 트리에 있는 노드의 차수 중에서 가장 큰 값 단말 노드(리스 노드) : 차수가 0인 노드로 자식 노드가 없는 노드 |
| 높이 | 노드의 높이 : 루트에서 노드에 이르는 간선의 수, 노드의 레벨 C의 높이 : 1, H의 높이 : 3 트리의 높이 : 트리에 있는 노드의 높이 중에서 가장 큰 값 |
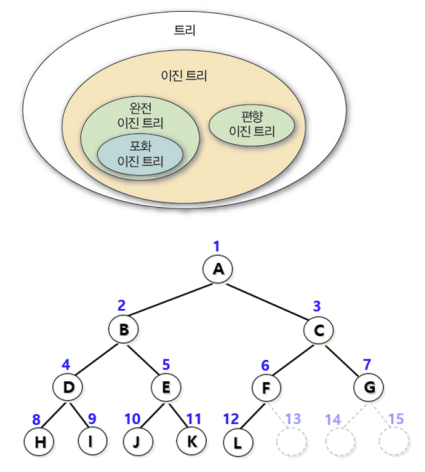
이진트리
1) 정의
- 트리의 모든 노드의 차수를 2 이하로 제한하여 전체 트리의 차수가 2 이하가 되도록 정의
- 이진 트리의 모든 노드는 왼쪽 자식 노드와 오른쪽 자식 노드만 가짐
이진트리 순회 ⭐⭐⭐
1) 정의
- 모든 원소를 빠트리거나 중복하지 않고 처리하는 연산
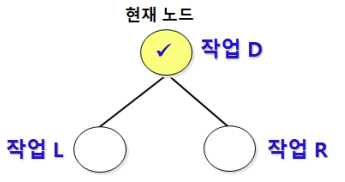
- 전위 순회/Preorder (D > L > R 순서/루트 노드가 제일 먼저)
- 중위 순회/Inorder (L > D > R 순서/루트 노드가 가운데)
- 후위 순회/Postorder (L > R > D 순서/루트 노드가 제일 마지막)
- 작업D : 현재 노드 처리
- 작업L : 현재 노드의 왼쪽 서브 트리로 이동
- 작업R : 현재 노드의 오른쪽 서브 트리로 이
그래프의 종류⭐
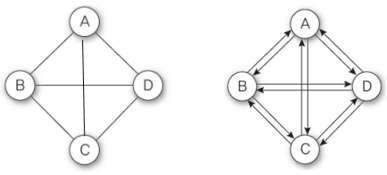
| 구분 | 설명 |
| 무방향 그래프 | 두 정점을 연결하는 간선에 방향이 없는 그래프 정점이 n개인 무방향 그래프에서 최대의 간선 수 : n(n-1)/2개 |
| 방향 그래프 | 간선에 방향이 있는 그래프 정점이 n개인 방향 그래프의 최대 간선 수 : n(n-1)개 |
빅-오 표기법 (Big-O notation)
1) 정의
- 아무리 많이 걸려도 이 시간 안에는 끝날 것
- 처리에 필요한 시간의 최대치
- 최악의 경우에도 정해진 수행 시간 안에는 알고리즘 수행 완료 보장
반정규화(Denormalization)
1) 정의
- 정규화에 충실하여 모델링을 소행하면 종속성, 활용성은 향상되나
수행속도가 증가하는 경우가 발생하여 이를 극복하기 위해 성능에 중점을 두어 정규화 하는 방법
2) 특징
- 데이터 모델링 규칙에 얽매이지 않고 수행한다
- 시스템이 물리적으로 구현되었을 때 성능향상을 목적으로 한다
반정규화(Denormalization) 유형
1) 중복 테이블 추가
* 용도
- 다량의 범위를 자주 처리하는 경우
- 특정 범위의 데이터만 자주 처리되는 경우
- 처리 범위를 줄이지 않고는 수행속도를 개선할 수 없는 경우
* 방법
- 집계 테이블 추가 : 활용하고자 하는 집계정보를 위한 테이블을 추가하고
각 원본테이블에 트리거를 등록시켜 생성하여 활용, 트리거의 오버헤드에 유의
- 진행 테이블 추가 : 이력관리 등의 목적으로 사용되며 활용도가 좋아지도록 기본키를 적절히 설정
- 특정 부분만을 포함하는 테이블 추가 : 거대한 테이블의 특정 부분만을 사용하는 경우
자주 사용되는 부분으로 새로운 테이블을 생성하여 활용
2) 테이블 조합
* 용도
- 대부분 처리가 두 개 이상의 테이블에 대해 항상 같이 일어나는 경우에 활용
* 방법
- 해당 테이블을 통합하여 설계
3) 테이블 분할
* 용도
- 컬럼의 사용빈도의 차이가 많은 경우
- 각각의 사용자가 각기 특정한 부분만 지속적으로 사용하는 경우
- 상황에 따라 SUPER-TYPE을 모두 내려 SUB-TYPE 별로 분할하거나 SUPER-TYPE만은 따로
테이블을 생성하는 경우
* 방법
- 수직 분할
- 수평 분할
4) 테이블 제거
* 용도
- 테이블 재정의나 칼럼의 중복화로 더 이상 액세스 되지 않는 테이블이 발생할 경우
* 방법
- 해당 테이블 삭제
5) 칼럼의 중복화
* 용도
- 자주 사용되는 칼럼이 다른 테이블에 분산되어 있어 상세한 조건에도 불구하고 액세스 범위를
줄이지 못한 경우
- 대량 데이터에서 Row별 연산 결과를 얻고자 할 때 성능향상을 위한 파생(Derived) 칼럼을 추가할 경우
- 기본키의 형태가 적절하지 않거나 너무 많은 칼럼으로 구성된 경우
- 정규화 규칙에 얽매이지 않으면서 성능향상을 목적으로 한 반정규화(Denormalization)를 통한
중복 데이터를 허용하는 경우
* 방법
- 필요한 해당 테이블이나 칼럼을 추가
정리하기
1. 선형 자료 구조
- 5 가지 : 순차리스트, 연결리스트, 스택, 큐, 데트
2. 트리 자료
- 노드(node), 간선(edge), 루트 노드, 형제 노드, 조상 노드, 서브 트리, 자손 노드, 차수(degree), 높이
3. 이진트리
- 트리의 모든 노드의 차수를 2 이하로 제한
4. 이진트리 순회⭐⭐⭐
- 전위 순회 (Preorder)
- 중위 순회 (Inorder)
- 후위 순회 (Postorder)
5. 그래프의 종류
- 무방향 그래프 : 방향이 없는 그래프, 간선 수 (n(n-1)/2개)
- 방향 그래프 : 방향이 있는 그래프, 간선 수 (n(n-1)개)
6. 빅-오 표기법 (Big-O notation)
- 처리에 필요한 시간의 최대치
- 정해진 수행 시간 안에는 알고리즘 수행 완료 보장
7. 반정규화 (Denormalization)
- 특징 : 데이터 모델링 규칙에 얽매이지 않음, 성능 향상이 목적
8. 반정규화 (Denormalization) 유형
- 중복 테이블 추가
- 테이블 조합
- 테이블 분할
- 테이블 제거
- 칼럼의 중복화
'정보처리기사 > 2과 소프트웨어 개발' 카테고리의 다른 글
| 5. 인터페이스 구현 (1) | 2023.09.23 |
|---|---|
| 4. 애플리케이션 테스트 관리 (0) | 2023.09.22 |
| 3. 소프트웨어 패키징 (0) | 2023.09.21 |
| 2. 통합 구현 (0) | 2023.09.20 |

